2012年造價工程師考試工程造價案例分析模擬自測題一
發布時間:2014-02-25 共1頁
模擬自測題一
| 一、案例分析題 |
| 1.某建設項目可行性研究階段擬定了兩個生產線方案,項目實施期為10年。 方案1:對原有生產線進行改造,投資200萬元,改造成功的概率為0.6。改造后前三年為投產試營期,綜合風險變化因素與生產效率預計每年凈現金流量為50萬元。 方案2:安裝新生產線,投資320萬元,項目成功概率為0.8。安裝后前3年為投產試營期,預計每年凈現金流量為60萬元。 若方案1、方案2均不成功,擬采用原生產線生產,并保持原生產線 水平(相關數據見表1-2-1)。兩方案設計效果有可能使產量增加或不變。根據市場調研,今后10年內產品的價格下跌的概率為0.1,保持不變的可能性為0.5,價格上升的概率為0.4。 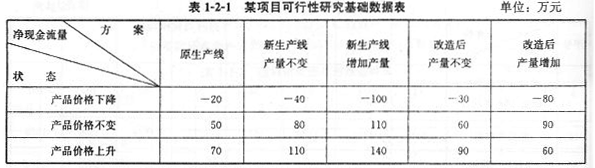 問題: 問題:假設今后10年內行業基準收益率為12%,以10年為項目計算期,試用決策樹分析法對上述方案進行評價。 |
| 正確答案: (1)繪制決策樹圖: 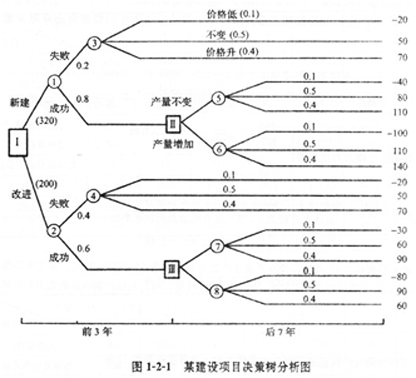 (2)計算: E(5)=[(-40)×0.1+80×0.5+110×0.4](P/A,12%,7)=80×4.5637=365.10(萬元) E(6)=[(-100)×0.1+1]0×0.5+140×0.4](P/A,12%,7)=101×4.5637=460.94(5/元) E(7)=[(-30)×0.1+60×0.5+90×0.4](P/A,12%,7)=63×4.5637=287.51(萬元) E(8)=[(-80)×0.1+90×0.5+60×0.4](P/A,12%,7)=61×4.5637=278.39(萬元) E(3)=[(-20)×0.1+50×0.5+70×0.4](P/A,12%,10)=51×4.5637=288.16(萬元) E(4)=E(3)=288.16(萬元) E(Ⅱ)=max{E(5),E(6)}=max{365.10,460.94}=460.94(萬元) E(Ⅲ)=max{E(7),E(8)}=max{287.51,278.39}=287.51(萬元) E(1)=[60×(P/A,12%,3)+E(Ⅱ)×(P/F,12%,3)]×0.8+E(3)×0.2-320=[60×2.402+460.94×0.712]×0.8+288.16×0.2-320=115.48(萬元) E(2)=[50×(P/A,12%,3)+E(Ⅲ)×(P/F,12%,3)]×0.6+E(4)×0.4-200=[50×2.402+287.51×0.712]×0.6+288.16×0.4-200=110.14(萬元) E(I)=max{E(1),E(2)}=115.48(萬元) 經計算應采取新建生產線方案。 |
- 2012年造價工程師考試工程造價案例分析習題集:四、建設工程施工招標投標
- 2012年造價工程師考試工程造價案例分析習題集:三、建設工程計量與計價
- 2012年造價工程師考試建設工程技術與計量(土建)習題集:六、工程計量(單項選擇題2)
- 2014年造價工程師工程計價考試試題及答案7
- 2015年造價工程師案例分析應注意的問題1
- 2011年造價工程師考試《理論與相關法規》真題解析
- 2012年造價工程師考試工程造價計價與控制習題集:五、建設項目招投標與合同價的簽訂
- 2014年造價工程師考試案例分析每日一練(3月26日)
- 2014年造價工程師工程計價考試試題及答案1
- 2013年造價工程師(計價與控制)習題及答案1

