09年統計師《統計工作實務》第九章輔導講義(3)
發布時間:2011-10-22 共1頁
① 移動平均法
通過對時間數列相鄰各項求平均數作為趨勢值或預測值的平滑或預測方法,稱為移動平均法。它具體可分為簡單移動平均法和加權移動平均法。
a. 簡單移動平均法
簡單移動平均法是將最近的K期數據加以平均,作為移動中項的趨勢測定值。
設移動時期項數為k,則第t期的移動平均值為:
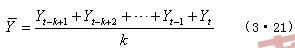
注意:當k取奇數或偶數的不同形式時,處理方法有區別。對于k取奇數時,可直接運用公式(3·12)即可;當k取偶數時,要在第一次對原數列作移動平均后,對所得新數列再做一次相鄰兩項的移動平均,這樣才能完成中心化。
例12 下表是1991-2000年我國的原煤產量數據,計算移動項數k=3,k=4時的反映趨勢變動的新數列。
表3-16 我國1991-2000年原煤產量數據
| 年份 | 1991 | 1992 | 1993 | 1994 | 1995 |
| 產量(億噸) | 10.87 | 11.16 | 11.50 | 12.40 | 13.61 |
| 年份 | 1996 | 1997 | 1998 | 1999 | 2000 |
| 產量(億噸) | 13.97 | 13.37 | 12.50 | 10.45 | 9.98 |
解:k=3時,移動項數為奇數,根據公式(3·21)得到
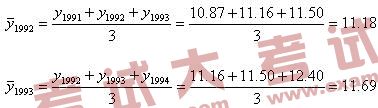
依此類推,最終結果匯集在表3-17中
當k=4時,移動項數為偶數,要移動兩次,第一次移動運用公式(3·21)
得到:
依此類推可得到表中第四列k=4時的第一次移動平均。這時求出的移動平均數還不能作為趨勢值,因為他們代表的時期不明確。因此要計算二次移動平均值來代表第三期的長期趨勢,即進行中心化。
第二步,對k=4時的第一次移動平均的結果(第四列)進行中心化處理。
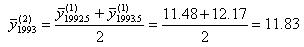
依此類推得到表3-17的第五列。
| 年份 | 產量 | 移動平均數 | ||
| K=3 | K=4 | |||
| 第一次移動平均 | 第二次移動平均 | |||
| 1991 | 10.87 | - | ||
| 1992 | 11.16 | 11.18 | 11.48 | |
| 1993 | 11.50 | 11.69 | 11.83 | |
| 1994 | 12.40 | 12.50 | 12.17 | 12.52 |
| 1995 | 13.61 | 13.33 | 12.87 | 13.15 |
| 1996 | 13.97 | 13.77 | 13.43 | 13.44 |
| 1997 | 13.73 | 13.40 | 13.45 | 13.06 |
| 1998 | 12.50 | 12.23 | 12.66 | 12.16 |
| 1999 | 10.45 | 10.98 | 11.67 | - |
| 2000 | 9.98 | - | - | |
從表3-17的計算結果看,我國的原煤產量經歷了先高后低的發展態勢。
a. 加權移動平均法
加權移動平均法是對各期指標值進行加權后計算移動平均數。在使用加權移動平均法時,一般計算奇數項加權移動數,各期權數以二項展開式為計算基礎,使得中項時期指標值的權數最大,兩邊對稱,越靠邊的項權值越小。