2012年初級會計職稱《初級會計實務》考試大綱(第十一章 財務管理基礎)
發布時間:2012-11-08 共1頁
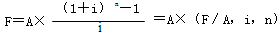
其中,
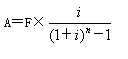
其中,![]() 稱為“償債基金系數”,記作(A/F,i,n)。
稱為“償債基金系數”,記作(A/F,i,n)。
3.普通年金現值
普通年金現值的計算實際上就是已知年金A,求普通年金現值P。
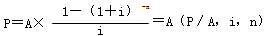
其中,![]() 稱為“年金現值系數”,記作(P/A,i,n),可直接查閱“年金現值系數表”。
稱為“年金現值系數”,記作(P/A,i,n),可直接查閱“年金現值系數表”。
4.年資本回收額的計算
6.即付年金現值 即付年金的現值就是把即付年金每個等額的A都換算成第一期期初的數值即第0期期末的數值,再求和。即付年金現值的計算就是已知每期期初等額收付的年金A,求現值P。 P=A×[(P/A,i,n-1)+1] 7.遞延年金終值 遞延年金的終值計算與普通年金的終值計算一樣,只是要注意期數。 F=A(F/A,i,n) 其中,n表示的是A的個數,與遞延期無關。 8.遞延年金現值 Po=A×(F/A,i,n)×(P/F,i,m+n) 9.永續年金的現值 永續年金的現值可以看成是一個n無窮大后付年金的現值,則永續年金現值計算如下: P(n→∞)=A[1一(1+i)-n]/i=A/i 當n趨向無窮大時,由于A、i都是有界量,(1+i)-n趨向無窮小, 因此P(n→∞)=A[1一(1+i)-n]/i趨向A/i。
年資本回收額是在約定年限內等額回收初始投入資本或清償所欠債務的金額。年資本回收額的計算實際上是已知普通年金現值P,求年金A。
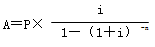
其中,![]() 稱為“資本回收系數”,記作(A/P,i,n)。
稱為“資本回收系數”,記作(A/P,i,n)。
5.即付年金終值的計算
即付年金的終值是把即付年金每個等額A都換算成第n期期末的數值,再來求和。
即付年金終值的計算公式為
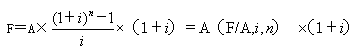
或F=A[(F/A,i,n+1)一1]
三、利率的計算
(一)復利計息方式下的利率計算
復利計息方式下,利率與現值(或者終值)系數之間存在一定的數量關系。已知現值(或者終值)系數,則可以通過內插法計算對應的利率。
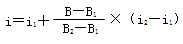
式中,所求利率為i,i對應的現值(或者終值)系數為B,B1、B2為現值(或者終值)系數表中B相鄰的系數,i1、i2為B1、B2對應的利率。
1.若已知復利現值(或者終值)系數B以及期數n,可以查“復利現值(或者終值)系數表”,找出與已知復利現值(或者終值)系數最接近的兩個系數及其對應的利率,按內插法公式計算利率。
2.若已知年金現值(或者終值系數)以及期數n,可以查“年金現值(或者終值)系數表”,找出與已知年金現值(或者終值)系數最接近的兩個系數及其對應的利率,按內插法公式計算利率。
3.永續年金的利率可以通過公式i=A/P計算。
(二)名義利率與實際利率
如果以“年”作為基本計息期,每年計算一次復利,這種情況下的年利率是名義利率。如果按照短于一年的計息期計算復利,并將全年利息額除以年初的本金,此時得到的利率是實際利率。名義利率與實際利率的換算關系如下:
i=(1+r/m)m一l
其中,i為實際利率;r為名義利率;m為每年復利計息次數。
第三節 風險與收益
一、資產的收益與收益率
資產的收益是資產的價值在一定時期的增值。一般情況下,有兩種表述資產收益的方式:一是以絕對數表示的資產價值的增值量,稱為資產的收益額;二是以相對數表示的資產價值的增值率,稱為資產的收益率或報酬率。
資產的收益額通常來源于兩個部分:一是一定期限內資產的現金凈收入;二是期末資產的價值(或市場價格)相對于期初價值(價格)的升值。前者多為利息、紅利或股息收益,后者稱為資本利得。
資產的收益率通常是以百分比表示的,是資產增值量與期初資產價值(或價格)的比值,該收益率也包括兩部分:一是利息(股息)的收益率;二是資本利得的收益率。
一般情況下,如果不做特殊說明的話,資產的收益均指資產的年收益率。
二、資產的風險
從財務管理的角度看,風險就是企業在各項財務活動過程中,由于各種難以預料或無法控制的因素作用,使企業的實際收益與預計收益發生背離,從而蒙受經濟損失的可能性。
資產的風險是資產收益率的不確定性,其大小可用資產收益率的離散程度來衡量。
資產收益率的離散程度是資產收益率的各種可能結果與預期收益率的偏差。
(一)資產的風險及其衡量
衡量風險的指標主要有收益率的方差、標準差和標準離差率等。
1.收益率的方差(σ2)
收益率方差是用來表示某資產收益率的各種可能結果與其期望值之間的離散程度的一個指標,其計算公式為:‘
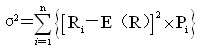
其中,E(R)表示資產的預期收益率,可用公式E(R)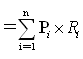 來計算;Pi是第i種可能情況發生的概率;Ri是在第i種可能情況下該資產的收益率。
來計算;Pi是第i種可能情況發生的概率;Ri是在第i種可能情況下該資產的收益率。
2.收益率的標準差(σ)
收益率標準差是反映了某資產收益率的各種可能結果對其期望值的偏離程度的一個指標。它等于方差的開方。
其計算公式為:
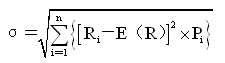
標準差和方差都是以絕對數衡量某資產的全部風險,在預期收益率(即收益率的期望值)相同的情況下,標準差或方差越大,風險越大;相反,在預期收益率相同的情況下標準差或方差越小,風險也越小。由于標準差或方差指標衡量的是風險的絕對大小,因而不適用于比較具有不同的預期收益率的資產的風險。
3.收益率的標準離差率(V)
標準離差率是收益率的標準差與期望值之比,也可稱為變異系數。其計算公式為:
V=σ/E(R)
標準離差率以相對數衡量資產的全部風險的大小,它表示每單位預期收益所包含的風險,即每一元預期收益所承擔的風險的大小。一般情況下,標準離差率越大,資產的相對風險越大;相反,標準離差率越小,相對風險越小。標準離差率可以用來比較具有不同預期收益率的資產的風險。
當不知道或者很難估計未來收益率發生的概率以及未來收益率的可能值時,可以利用收益率的歷史數據去近似地估算預期收益率及其標準差。其中預期收益率可利用算術平均法等來計算,標準差可以利用下列統計中的公式進行估算: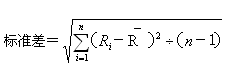
其中,Ri表示數據樣本中各期的收益率的歷史數據;是各歷史數據的算術平均值;n表示樣本中歷史數據的個數。
(二)風險控制對策
1.規避風險
當資產風險所造成的損失不能由該資產可能獲得的收益予以抵銷時,應當放棄該資產,以規避風險。
2.減少風險
減少風險主要有兩方面的意思:一是控制風險因素,減少風險的發生;二是控制風險發生的頻率和降低風險損害程度。
3.轉移風險
對可能給企業帶來災難性損失的資產,企業應以一定的代價,采取某種方式轉移風險。
4.接受風險
接受風險包括風險自擔和風險自保兩種。風險自擔是風險損失發生時,直接將損失攤入成本或費用,或沖減利潤;風險自保是企業預留一筆風險金或隨著生產經營的進行,有計劃地計提資產減值準備等。
三、風險偏好
根據人們的效用函數的不同,可以按照其對風險的偏好分為風險回避者、風險追求者和風險中立者。
(一)風險回避者
風險回避者選擇資產的態度是:當預期收益率相同時,偏好于具有低風險的資產;而對于具有同樣風險的資產,則偏好于具有高預期收益的資產。
(二)風險追求者
與風險回避者恰恰相反,風險追求者主動追求風險,喜歡收益的動蕩勝于喜歡收益的穩定。他們選擇資產的原則是:當預期收益相同時,選擇風險大的,因為這會給他們帶來更大的效用。
(三)風險中立者
風險中立者既不回避風險,也不主動追求風險。他們選擇資產的唯一標準是預期收益的大小,而不管風險狀況如何。

