2012年一級注冊結構工程師考試普通物理考前沖刺(二)
發布時間:2012-07-25 共1頁
考前沖刺(二)
| 一、單選題 |
1.有兩種理想氣體,第一種的壓強記作P.gif) ,體積記作V ,體積記作V.gif) ,溫度記作T ,溫度記作T.gif) ,總質量記作m ,總質量記作m.gif) ,摩爾質量記作M ,摩爾質量記作M.gif) ;第二種的壓強記作P ;第二種的壓強記作P.gif) ,體積記作V ,體積記作V.gif) ,溫度記作T ,溫度記作T.gif) ,總質量記作m ,總質量記作m.gif) ,摩爾質量記作M ,摩爾質量記作M.gif) 。當P 。當P.gif) =P =P.gif) ,V ,V.gif) =V =V.gif) ,T ,T.gif) =T =T.gif) 時,則 時,則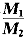 為( )。 為( )。 |
| 正確答案:C 解題思路:【解析】設理想氣體的壓強為P,體積為V,溫度為T,質量為m,摩爾質量為M,摩爾氣體常量為R,則理想氣體狀態方程為PV=(m/M)RT。可得氣體的摩爾質量M為: M=mRT/PV對兩種理想氣體,當P .gif) =P =P.gif) ,V ,V.gif) =V =V.gif) ,T ,T.gif) =T =T.gif) 時,則摩爾質量之比為:M 時,則摩爾質量之比為:M.gif) /M /M.gif) =m =m.gif) /m /m.gif) ;故選擇答案C。 ;故選擇答案C。【點評】本題主要考察理想氣體狀態方程PV=(m/M)RT,可推導出氣體的摩爾質量為:M=mRT/PV,然后根據已知條件即可得到正確答案。 |
|
|
| 2.質量一定的理想氣體,從相同狀態出發,分別經歷等溫過程、等壓過程和絕熱過程,使其體積增加一倍。那么氣體溫度的改變(絕對值)在( )。 |
正確答案:D 解題思路:【解析】設初始氣體體積V.gif) ,溫度T ,溫度T.gif) ,壓強P ,壓強P.gif) 末狀態氣體體積V,溫度T,壓強P。對等壓過程:V/T=V 末狀態氣體體積V,溫度T,壓強P。對等壓過程:V/T=V.gif) T T.gif) ∵V=2V .gif) ∴T=2T .gif) ,氣體溫度的改變|△T|=T ,氣體溫度的改變|△T|=T.gif) 對等溫過程:氣體溫度的改變|△T|=0 對絕熱過程:TV  =T =T.gif) V V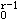 ∵V=2V .gif) ∴T=(1/2)[~r-1]T .gif) |△T|<T |△T|<T.gif) ; ;所以,溫度的改變(絕對值)在等壓過程最大,等溫過程中最小。 【點評】考察等壓過程,等溫過程,絕熱過程的特點和過程方程。 |
|
|
| 3.1mol剛性雙原子分子氣體,當溫度為T時,其內能為( )。 |
正確答案:B 解題思路:【解析】由能量均分原理可知,氣體分子任一自由度的平均能量都等于(1/2)kT,如果氣體分子有i個自由度,則每個分子的總平均動能是(i/2)kT。1mol理想氣體有N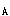 個分子,所以1mol理想氣體的內能是:E=N 個分子,所以1mol理想氣體的內能是:E=N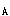 ·(i/2)kT=(i/2)RT;因為剛性雙原子分子氣體有5個自由度,即i=5,所以1mol剛性雙原子分子氣體,當溫度為T時,其內能為E=(i/2)RT=(5/2)RT;故選擇答案B。 ·(i/2)kT=(i/2)RT;因為剛性雙原子分子氣體有5個自由度,即i=5,所以1mol剛性雙原子分子氣體,當溫度為T時,其內能為E=(i/2)RT=(5/2)RT;故選擇答案B。【點評】本題主要考查分子自由度的概念、能量均分原理和理想氣體的內能公式。雙原子氣體分子有5個自由度。能量均分原理是指:氣體分子任一自由度的平均能量都等于專尼T,如果氣體分子有i個自由度,則每個分子的總平均動能是(i/2)kT。1mol理想氣體的內能公式是:E=N  ·(i/2)kT=(i/2)RT質量為m,摩爾質量為M的理想氣體內能公式是:E=m/M·(i/2)RT=ν·(i/2)RT上式中ν為摩爾數。 ·(i/2)kT=(i/2)RT質量為m,摩爾質量為M的理想氣體內能公式是:E=m/M·(i/2)RT=ν·(i/2)RT上式中ν為摩爾數。 |
|
|
4.由圖(a)t=0時的波形圖和圖(b)P點處振動圖,可得波動方程為( )。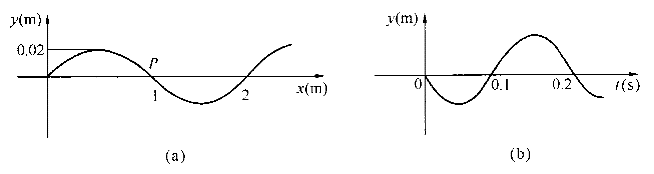 |
| 正確答案:D 解題思路:【解析】由圖(a)知,振幅A=0.02m,波長λ=2m。由圖(b)知,周期T=0.2s,且P點向下(y負方向)運動,由波形圖知波向左傳播。波速u=λ/T=10m/s,ω=2π/T=10π。 令波動方程為 y=Acos[ω(t+x/u)+φ] 代入數值得波動方程為 y=0.02cos(t+x/10)+φ] 下面確定初相φ。 將P點坐標x=1m,以及t=0,代入波動方程得0.02cos[10π(t+1/10)+φ]=0 解得: φ=±π/2 上式中φ=+π/2的根舍去,這是因為P點向下(y負方向)運動,即t=0時,x=1m處P點的速度為負值。將這些數值代入P點的振動速度公式, 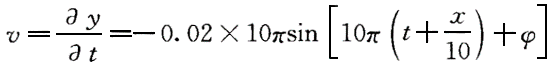 由上式可得 由上式可得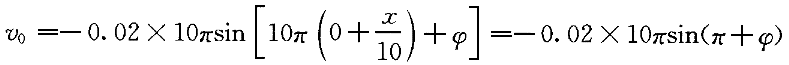 根據υ 根據υ.gif) <0,可以判斷出初相為 <0,可以判斷出初相為φ=-π/2所以,波動方程為 y=0.02cos[10π(t+x/10)-π/2] 【點評】根據波形圖可以確定波長(λ),振幅(A)。根據某點P振動圖可以確定周期(T)代入波速u=λ/T,角頻率ω=2π/T等求出波速和角頻率。根據某點P振動圖,判斷P在t=0時運動方向,再根據波形圖可以判斷波的傳播方向。根據初始條件(t=0時,初位移y=y .gif) ,初速度υ=υ ,初速度υ=υ.gif) )求解初相φ。運用待定系數法,設波動方程為y=Acos[ω(t-x/u)+φ],分別將求得振幅(A)、波速(u)、角頻率ω、初相φ代入方程即可求解。 )求解初相φ。運用待定系數法,設波動方程為y=Acos[ω(t-x/u)+φ],分別將求得振幅(A)、波速(u)、角頻率ω、初相φ代入方程即可求解。 |
|
|
5.從兩相干光源s.gif) 與s 與s.gif) 發出的相干光,在與s 發出的相干光,在與s.gif) 、s 、s.gif) 等距離d的p點相遇。若s 等距離d的p點相遇。若s.gif) 位于真空中,s 位于真空中,s.gif) 位于折射率為n的介質中,p點位于界面上,計算s 位于折射率為n的介質中,p點位于界面上,計算s.gif) 和s 和s.gif) 到p點的光程差( )。 到p點的光程差( )。 |
| 正確答案:B 解題思路:【解析】由光程差定義得δ=nd=d-d=(n-1)d 【點評】光波在介質中的路程x相當于在真空中的路程nx。所以將光波在某一介質j所經歷的幾何路程d與這介質的折射率n的乘積nd,稱為光程,即:L=nd;光程差定義為兩光程的差值,即光程差公式為:δ=△L=L .gif) -L -L.gif) 。 。 |

