2012年一級注冊結構工程師考試理論力學考前沖刺(五)
發布時間:2012-07-25 共1頁
考前沖刺(五)
| 一、單選題 |
1.如圖所示系統的自由度數為( )。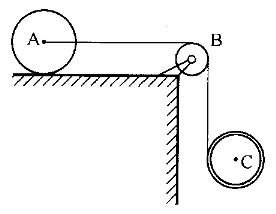 |
| 正確答案:A 解題思路:【解析】系統的自由度為A輪的轉動和水平移動,B輪的轉動以及C輪的轉動和豎向移動。 【點評】本題主要考察體系自由度的概念及其確定方法。 |
|
|
2.自重為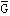 的小球在繩索和光滑斜面的約束下處于靜止,分析圖示三種情況下斜面對小球的支持力 的小球在繩索和光滑斜面的約束下處于靜止,分析圖示三種情況下斜面對小球的支持力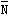 的大小,經對比,他們之間的關系應是( )。 的大小,經對比,他們之間的關系應是( )。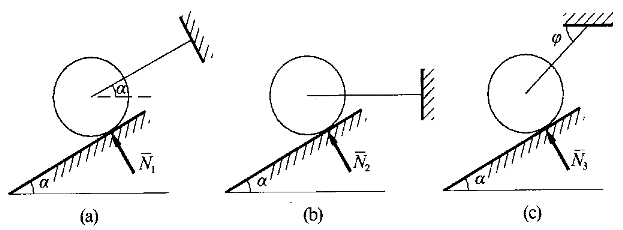 |
正確答案:B 解題思路:【解析】畫出三種情況下小球的受力圖則分別有:N.gif) =G·cosα、N =G·cosα、N.gif) ·cosα=G、T·sinθ+N ·cosα=G、T·sinθ+N.gif) ·cosa-G,其中T為繩中拉力,比較以上三式可得正確答案。 ·cosa-G,其中T為繩中拉力,比較以上三式可得正確答案。【點評】本題主要考察平面匯交力系的合成與分解。 |
|
|
3.在點的合成運動中,式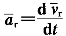 成立的條件是牽連運動為( )。 成立的條件是牽連運動為( )。 |
| 正確答案:A 解題思路:【解析】牽連運動為平動時,科氏加速度為零。 【點評】本題主要考察點的加速度合成的概念。 |
|
|
4.用鋼楔劈物,接觸面間的摩擦角為φ ,鋼楔重力不計。劈入后欲使鋼楔不滑出,鋼楔兩個平面的夾角α應為( )。 ,鋼楔重力不計。劈入后欲使鋼楔不滑出,鋼楔兩個平面的夾角α應為( )。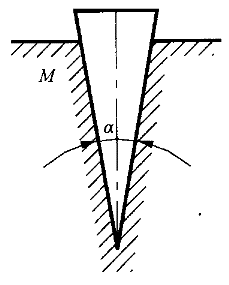 |
正確答案:D 解題思路:【解析】當鋼楔處于臨界狀態時,兩斜面處的全反力與斜面法線間的夾角為摩擦角φ 。故應有α≤2φ 。故應有α≤2φ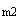 。 。【點評】本題主要考察對于摩擦中自鎖現象的理解。 |
|
|
5.平面力系向1點簡化時,主矢量 .gif) =0,主矩M =0,主矩M.gif) ≠0,如果將該力系向另一點2簡化,則主矢量 ≠0,如果將該力系向另一點2簡化,則主矢量 .gif) 和主矩M 和主矩M.gif) 為( )。 為( )。 |
正確答案:C 解題思路:【解析】平面力系向一點簡化時,若主矢量R.gif) =0,主矩M =0,主矩M.gif) ≠0,則該力系的簡化結果與簡化中心位置無關,不論向哪一點簡化,結果都是一個相同大小的力偶。 ≠0,則該力系的簡化結果與簡化中心位置無關,不論向哪一點簡化,結果都是一個相同大小的力偶。【點評】本題主要考察平面一般力系的簡化,及其結果的討論。 |
|
|
| 二、單選題 |
| (6-9題共用題干) |
圖示直角剛性彎桿OAB由OA和AB桿固結而成,均質桿AB的質量為m,桿OA的質量不計。圖示瞬時剛性彎桿繞O軸轉動的角速度為ω,角加速度為ε。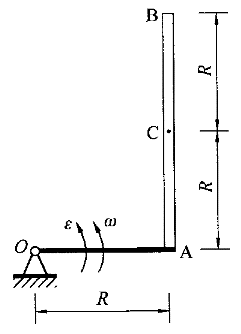 |
| 6.該瞬時體系的動量大小為( )。 |
| 7.該瞬時桿件OAB對O軸的動量矩的大小為( )。 |
| 8.該瞬時剛性彎桿的動能大小為( )。 |
9.將該瞬時桿件上的慣性力向O點簡化的主矢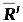 和主矩 和主矩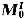 的數值為( )。 的數值為( )。 |
正確答案:6.C;7.D;8.B;9.D 解題思路:1.【解析】質點系的動量等于質點系的質量與其質心速度的乘積,質心速度:υ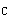 = =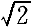 Rω Rω【點評】本題主要考察質點系動量的概念。 2.【解析】桿件OAB對O軸的動量矩L  =J =J.gif) 。叫,其中,J 。叫,其中,J 為剛性彎桿對O軸的轉動慣量J 為剛性彎桿對O軸的轉動慣量J =(1/2)m(2R) =(1/2)m(2R) +m·OA +m·OA 。 。【點評】本題主要考察定軸轉動剛體動量矩的概念,剛體轉動慣量的計算以及平行軸定理。 3.【解析】繞定軸轉動剛體的動能T=(1/2)J .gif) [~2.]其中,J [~2.]其中,J 為桿件對O軸的轉動慣量,J 為桿件對O軸的轉動慣量,J.gif) =(1/12)m(2R) =(1/12)m(2R) +m·OA +m·OA 。 。【點評】本題主要考察繞定軸轉動剛體動能的計算公式。 4.【解析】桿件作繞定軸轉動, 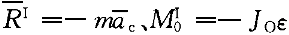 ,其中 ,其中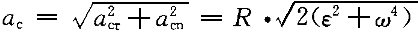 ,桿件繞O軸的轉動慣量J ,桿件繞O軸的轉動慣量J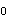 =(1/12)m(2R) =(1/12)m(2R).gif) +m·OA +m·OA.gif) 。 。【點評】本題考察的知識點是:慣性力與慣性力偶的基本概念;剛體繞定軸轉動時慣性力系的簡化。 |
|
|
| (10-11題共用題干) |
繩索AB繞過園滑輪C,輪軸O通過滑輪中心且與滑輪光滑接觸,繩索及滑輪重量不計。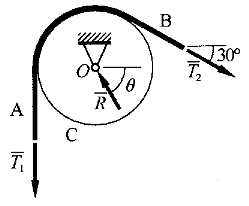 |
10.索中的拉力 .gif) 、 、 .gif) 滿足的關系為( )。 滿足的關系為( )。 |
11.若T.gif) 為豎直方向,T 為豎直方向,T.gif) 與水平方向夾角為30°,則輪軸O處的支座反力的大小及方向為( )。 與水平方向夾角為30°,則輪軸O處的支座反力的大小及方向為( )。 |
正確答案:10.C;11.A 解題思路:1.【解析】將滑輪與繩索一起作為考察對象, .gif) 、 、 .gif) 、 、 匯交于一點,由于 匯交于一點,由于 .gif) 、 、 .gif) 沿著輪緣的切線方向,所以 沿著輪緣的切線方向,所以 與 與 .gif) 、 、 .gif) 夾角必相等,畫出 夾角必相等,畫出 、 、 .gif) 、 、.gif) 的力多邊形為自行封閉的等腰三角形,從而有T 的力多邊形為自行封閉的等腰三角形,從而有T.gif) =T =T.gif) 。 。【點評】在考慮繩索跨過滑輪的平衡問題時,一般總要將滑輪與繩索作為整體來考慮,同時注意,繩中拉力始終應沿著輪緣的某一切線方向。 2.【解析】將滑輪與繩索一起作為考察對象, .gif) .gif) 、 、 .gif) 、 、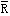 匯交于一點,由圖解法或解析法求解合力。 匯交于一點,由圖解法或解析法求解合力。【點評】本題考察平面匯交力系的合成。 |

