2012年巖土工程師考試基礎知識模擬試題:理論力學(單項選擇題1)
發布時間:2012-07-25 共1頁
理論力學(單項選擇題1)
| 一、單項題的備選項中只有一個最符合題意,錯選、多選均不得分。 |
1.圖4-5(a)所示機構由兩曲柄O A和O A和O B,半圓形平板ACB及鉛直桿CD組成,它們都在圖示平面內運動。已知曲柄O B,半圓形平板ACB及鉛直桿CD組成,它們都在圖示平面內運動。已知曲柄O A以勻角速度ω= A以勻角速度ω= rad/s繞軸O rad/s繞軸O 朝逆時針方向轉動,O 朝逆時針方向轉動,O A=O A=O B=15cm,O B=15cm,O O O =AB,半圓形平板的半徑r= =AB,半圓形平板的半徑r=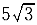 cm,O cm,O 和O 和O 位于同一水平線上。則在圖示位置時,CD桿的加速度a 位于同一水平線上。則在圖示位置時,CD桿的加速度a 為( )。 為( )。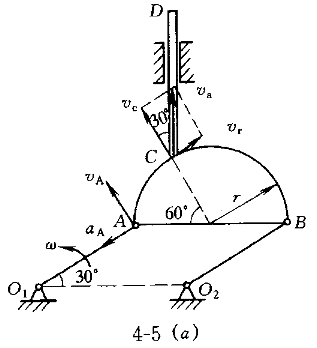 |
正確答案:B 解題思路:解:由于O A=O A=O B,O B,O O O.gif) =AB,故半圓形平板ACB作平動。取CD桿上的C點為動點,動系與半圓形平板固連(平動系)。于是 =AB,故半圓形平板ACB作平動。取CD桿上的C點為動點,動系與半圓形平板固連(平動系)。于是v  =v =v a  =a =a A點的速度和加速度大小分別為 v  =OA·ω=15· =OA·ω=15· =15 =15.gif) cm/s cm/sa  =OA·ω =OA·ω =15·( =15·(.gif) ) ) =15 =15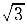 cm/s cm/s 它們的方向如圖5所示。 根據已知條件和速度合成定理,作出動點的速度平行四邊形如圖5(a)所示,從而可得: v  =v =v etan30°=v etan30°=v Atan30° Atan30°= 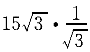 =15cm/s =15cm/s標出動點C的各項加速度如圖4-5(b)所示,并選圖示坐標系czy。 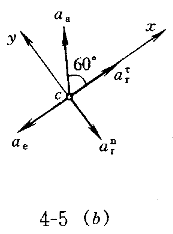 根據牽連運動為平動時點的加速度合成定理,此時有: 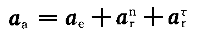 將此矢量式向圖示y軸投影,得: 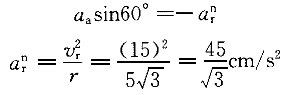 于是 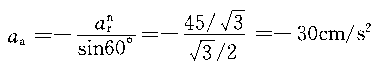 a  為負值,說明a 為負值,說明a 在圖上所設指向與實際情況相反,即a 在圖上所設指向與實際情況相反,即a 的方向鉛直向下。所得a 的方向鉛直向下。所得a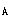 即為此時CD桿的加速度a 即為此時CD桿的加速度a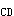 。 。故應選擇B。 |
|
|
2.圖4所示機構中,曲柄OB朝逆時針向轉動,并帶動桿AC,該桿上點A和滑塊在水平滑槽內運動。已知:AB=OB=20cm;BC=40cm,曲柄OB與鉛直線的夾角φ=4t(t以秒計),則當φ=π/2時,AC桿上C點的速度大小v 為( )。 為( )。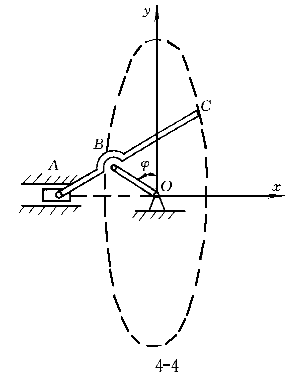 |
| 正確答案:D 解題思路:解:取圖示直角坐標系Oxy,由題意知,在任意瞬時t,曲柄OB與y軸的夾角ψ=4t,且△ABO是等腰三角形,∠BAO=∠BOA=π/ψ。于是,由幾何關系可得C點的運動方程為: x=ACcos(π/ψ)-(AB+OB)cos(π/ψ) =(20+40)sinψ-(20+20)sinψ =20sinψ==20sin4t y=ACsin(π/ψ)=(20+40)cosψ =60cosψ==60cos4t從而可得 v  = =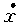 =20·4cos4t=80cos4t =20·4cos4t=80cos4tv  = =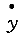 =60·4sin4t=-240sin4t =60·4sin4t=-240sin4t當ψ=4t=π/2時,有 v 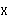 =0 =0v 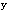 =-240cm/s =-240cm/s所以,此時C點的速度大小為 v= 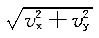 =240cm/s =240cm/s故應選擇D。 |
|
|
3.圖9所示一重量為W、半徑為r的均質圓柱,沿一半徑為R的圓柱面上作純滾動,圓柱體在圓柱面最低點A附近作微小振動時的固有圓頻率p為( )。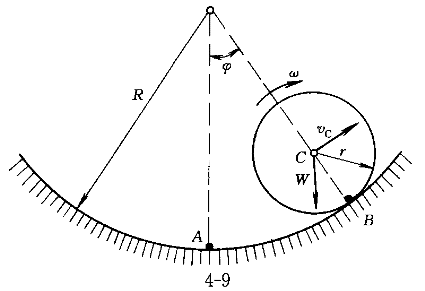 |
正確答案:B 解題思路:解:取ψ為廣義坐標,以靜平衡位置為勢能的零位置。因重力為有勢力,圓柱滾而不滑時約束力不作功,所以可用機械能守恒定理建立運動微分方程。由vc=(R-r) 和vc=rω 和vc=rω可知ω=R-r  /r /r其動能為 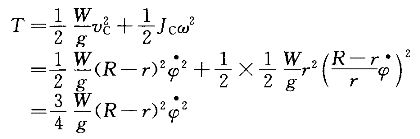 勢能為V=W[R-r-(R-r)cosψ] 由機械能守恒定理T+V=const,有  +W[R-r-(R-r)cosψ]=const +W[R-r-(R-r)cosψ]=const將上式兩邊對t求導,再消去公因子 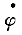 得 得 +W(R-r)Sinψ=0 +W(R-r)Sinψ=0當ψ微小時,sin≈ψ,得  +2gψ/3(R-r)=0 +2gψ/3(R-r)=0從而得知p=  故應選擇B。 |
|
|
4.圖7所示OA桿繞O軸朝逆時針向轉動,均質圓盤沿OA桿滾動而無滑動。已知圓盤的質量m=20kg,半徑R=10cm。在圖示位置時,OA桿的傾角為30°,其轉動的角速度ω.gif) =1rad/s,圓盤相對OA桿轉動的角速度ω =1rad/s,圓盤相對OA桿轉動的角速度ω.gif) =4rad/s,OB= =4rad/s,OB= cm,則此時圓盤的動量大小為( )。 cm,則此時圓盤的動量大小為( )。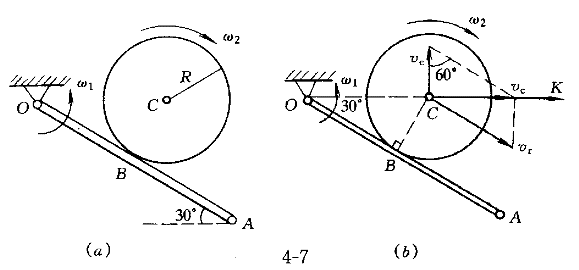 |
| 正確答案:D 解題思路:解:先用點的合成運動的方法求圓盤質心C的絕對速度vC。取C點為動點,動系選為與OA桿固連的轉動系,根據已知條件和速度合成定理,作出動點C的速度平行四邊形如圖7(b)。而 v[e.gf]=OC·ω .gif) =R/sin30°·ω =R/sin30°·ω.gif) =10/0.5×1=20cm/s =10/0.5×1=20cm/sv 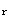 =R·ω =R·ω.gif) =10×4=40cm/s =10×4=40cm/s從而得知v  ⊥v ⊥v.gif) ,于是有 ,于是有v  =v =v tan60°= tan60°= cm/s cm/s所以,圓盤的動量大小為 K=mv  =20· =20·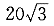 = =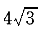 N·s N·sK的方向水平向右。 故應選擇D。 |
|
|
5.一繩索跨過均質定滑輪B,繩的一端掛一重物A;另一端纏繞一均質圓柱C,如圖8(a)所示。已知重物A的質量為mA;定滑輪B和圓柱C的質量分別為mB和mc,它們的半徑均為r。繩的質量略去不計,它對定滑輪無相對滑動。設m =m =m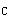 =2m =2m ,則定滑輪與圓柱之間繩索的拉力T為( )。 ,則定滑輪與圓柱之間繩索的拉力T為( )。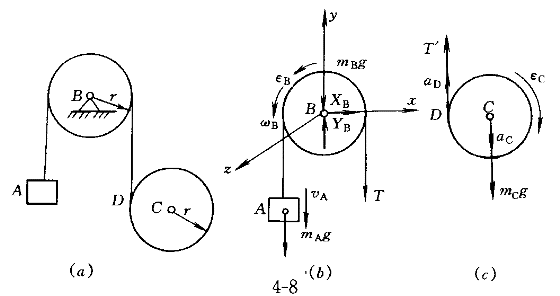 |
正確答案:A 解題思路:解:以定滑輪B連同重物A為研究對象,其受力圖和所取直角坐標系Bxyz如圖8(6)所示。由動量矩定量dH /dt=Em /dt=Em (F (F )有 )有d/dt(1/2mBr  ·ωB+mAvA·r)=mAg·r-T·r ·ωB+mAvA·r)=mAg·r-T·r將m  =2mA和v =2mA和v =rωB.gif]代入,并注意到dω =rωB.gif]代入,并注意到dω /dt=ε /dt=ε 有 有2m  r r.gif) ε ε =m =m gr-Tr即T=m gr-Tr即T=m g-2m g-2m rε rε (1) (1)再取圓柱C為研究對象,其受力圖如圖8(c)。由剛體平面運動微分方程有 mcac=mcg-T′ 1/2mcr .gif) ·εc=T′·r ·εc=T′·r將mc=2m  、T′=T和ac=rεc=ad=rεc-rε 、T′=T和ac=rεc=ad=rεc-rε 代入,有 代入,有2m  ·r(εc-ε ·r(εc-ε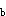 )=2m )=2m g-T(2)m g-T(2)m.gif) r r.gif) εc=Tr(3) εc=Tr(3)由式(1)~式(3)三式聯立解得 T=3/4m 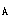 g g故應選擇A。 |
- 2012年巖土工程師考試基礎知識模擬試題:工程地質(單項選擇題1)
- 2012年巖土工程師考試基礎知識模擬試題:理論力學(單項選擇題1)
- 2012年巖土工程師考試基礎知識模擬試題:高等數學(單項選擇題3)
- 2012年巖土工程師考試專業知識考前沖刺(五)上午卷
- 2016年巖土工程師考試《綜合知識》沖刺練習(4)
- 2012年巖土工程師考試基礎知識模擬試題:彈性力學和結構力學(單項選擇題2)
- 2016年巖土工程師考試《綜合知識》沖刺練習(3)
- 2012年巖土工程師考試基礎知識模擬試題:電工與電子技術(單項選擇題2)
- 土工結構、邊坡與支擋結構、基坑與地下工程(單項選擇題2)
- 2016年巖土工程師考試《綜合知識》沖刺練習(5)

