2017國家公務員考試行測技巧:數學運算之十字交叉法
發布時間:2016-10-11 共1頁
【例題】濃度為10%的酒精溶液A和濃度為50%的酒精溶液B混合后濃度變為25%,則這A、B兩種溶液的量的比值是多少?
【解析】根據我們的方程思想,混合前后的溶質也就是酒精的量是一樣的,設A溶液有aml,B溶液有bml,則有a×10%+b×50%=(a+b)×25%,
可得a(25%-10%)=b(50%-25%)
可以求得a:b=(50%-25%):(25%-10%)=5:3
實際上,我們可以將其變化形式,得到我們的十字交叉法,如下:
部分平均量總體平均量均值差最簡比
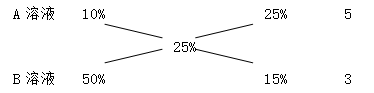
得到的最簡比5:3,根據剛才列方程的計算過程,我們知道它就是兩種溶液的量的比值。
上述方法就是十字交叉法,到底哪些題目可以用十字交叉法呢?通過觀察我們會發現,題目存在兩個部分,經混合后得到一個整體。符合這樣條件的題目,都是可以用十字交叉法來做的。這里面有個知識點需要注意就是得到的最簡比到底是什么的比值?假設平均量=m/n,那么得到的最簡比就是n所代表的量的比值。在這里一共有5個量,已知其中任何4個量,都可以求出第五個量。
【例如】某次期末考試后,A班級的平均分為75,B班級的平均分為84,兩個班級的總平均分為81,則兩個班級的人數之比為多少?
【中公解析】觀察題目,總平均分是由兩個班級混合得到的,所以可以用十字交叉法。如下:
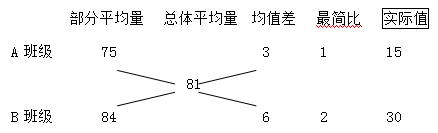
本題中,部平均量為平均分,平均分=總分/人數,所以得到的最簡比就是人數之比為1:2.如果已知A班級人數為15人,則可以得到B班級人數為30人。在做題過程中,可以在上述圖例中再添加一列叫實際值。
接下來看一道十字交叉法在利潤問題中的應用
【例題】一批商品,按期望獲得50%的利潤來定價。結果只售出70%的商品,為盡早售完剩下的商品,商店決定按定價打折銷售,這樣所獲得的全部利潤是原來的期望利潤的82%,問打了幾折?
【中公解析】最終的利潤率50%×82%=41%是由兩部分混合得到的,一部分是70%商品的利潤率,一部分是剩下30%商品的利潤率,所以設打折后商品的利潤率為x%。則有

所以有(41%-x%):9%=7:3,x%=20%
即打折后的利潤率為20%,假設商品成本為100,則打折前售價為150,打折后售價為120,則打折率為120/150=80%。
【提醒】總利潤率=總利潤/總成本,所以得到的最簡比應該是總成本的比值,總成本=單個成本×數量,單個成本一樣,所以得到的最簡比也就是打折前后的數量之比。
十字交叉法的應用很廣泛,專家希望考生在平時訓練做題的時候,應該多觀察多思考從不同的路徑解決題目。

