證券投資分析第七章重點講義(1) 證券組合管理概述
發布時間:2012-11-13 共1頁
第一節 證券組合管理概述
證券組合管理理論最早是由美國著名經濟學家哈里·馬柯威茨于1952年系統提出。
一、證券組合含義和類型
“組合”一詞通常是指個人或機構投資者所擁有的各種資產的總稱。
證券組合按不同的投資目標可以分為避稅型、收入型、增長型、收入和增長混合型、貨幣市場型、國際型及指數化型等。
二、證券組合管理的意義和特點
證券組合管理的意義在于:采用適當的方法選擇多種證券作為投資對象,以達到在保證預定收益的前提下使投資風險最小或在控制風險的前提下使投資收益最大化的目標,避免投資過程的隨意性。
證券組合管理特點主要表現在兩個方面:
(1)投資的分散性。
(2)風險與收益的匹配性。高風險,高收益。
三、證券組合管理的方法和步驟
(一)證券組合管理的方法
根據組合管理者對市場效率的不同看法,其采用的管理方法可大致分為被動管理和主動管理兩種類型。
被動管理,指長期穩定持有模擬市場指數的證券組合以獲得市場平均收益的管理方法。
主動管理,指經常預測市場行情或尋找定價錯誤證券,并借此頻繁調整證券組合以獲得盡可能高的收益的管理方法。
(二)證券組合管理的基本步驟
四、現代證券組合理論體系的形成與發展
(一)現代證券組合理論的產生
1952年,哈理·馬柯威茨發表了一篇題為《證券組合選擇》的論文。這篇著名的論文標志著現代證券組合理論的開端。第一次對證券投資中的風險因素進行了正規的闡述。思想是中庸之道,收益和風險的均衡。
(二)現代證券組合理論的發展
缺點:計算量太大。
夏普、特雷諾、詹森分別于1964、1965、1966年提出了著名的資本資產定價模型(CAPM)。1976年,理查德·羅爾對這一模型提出了批評,因這該模型永遠無法用經驗事實來檢驗。史蒂夫·羅斯突破性地發展了資本資產定價模型,提出套利定價理論(APT)。羅爾和羅斯在1984年認為這一理論至少在原則上是可以檢驗的
第二節 證券組合分析
一、單個證券的收益和風險
(一)收益及其度量 、
在股票投資中,投資收益等于期內股票紅利收益和價差收益之和,其收益率計算公式為:

在股票投資中,投資收益等于期內股票紅利收益和價差收益之和,其收益率計算公式為:

(二)風險及其度量
風險的大小由未來可能收益率與期望收益率的偏離程度來反映。這種偏離程度由收益率的方差來度量。

式中,Pi--可能收益率發生的概率;
σ――標準差
二、證券組合的收益和風險
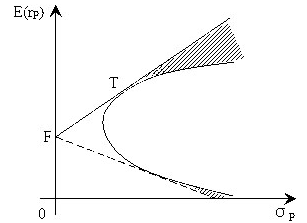
三、證券組合的可行域和有效邊界
(一)證券組合的可行域
1.兩種證券組合的可行域
(1)完全正相關下的組合線;
(2)完全負相關下的組合線;
(3)不相關情形下的組合線;
(4)組合線的一般情形。
從組合線的形狀來看,相關系數越小,在不賣空的情況下,證券組合的風險越小,特別是負完全相關的情況下,可獲得無風險組合。在不賣空的情況下,組合降低風險的程度由證券間的關聯程度決定。
2.多種證券組合的可行域
可行域的形狀依賴于可供選擇的單個證券的特征E(ri)和σi以及它們收益率之間的相互關系ρij,還依賴于投資組合中權數的約束。
可行域滿足一個共同的特點:左邊界必然向外凸或呈線性,也就是說不會出現凹陷。
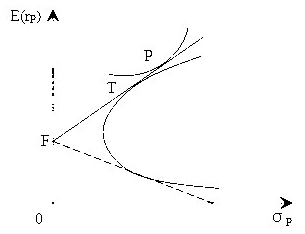
(二)證券組合的有效邊界
四、最優證券組合
(一)投資者的個人偏好與無差異曲線
一個特定的投資者,任意給定一個證券組合,根據他對風險的態度,可以得到一系列滿意程度相同(無差異)的證券組合這些組合恰好形成一條曲線,這條曲線就是無差異曲線。
無差異曲線都具有如下六個特點:
1.無差異曲線是由左至右向上彎曲的曲線;
2.每個投資者的無差異曲線形成密布整個平面又互不相交的曲線簇。
3.同一條無差異曲線上的組合給投資者帶來的滿意程度相同。
4.不同無差異曲線上的組合給投資者帶來的滿意程度不同。
5.無差異曲線的位置越高,其上的投資組合帶來的滿意程度就越高。
6.無差異曲線向上彎曲的程度大小反映投資者承受風險的能力強弱。
(二)最優證券組合的選擇
最優證券組合是使投資者最滿意的有效組合,它恰恰是無差異曲線簇與有效邊界的切點所表示的組合。

